Entropía

 La entropía (S) es una magnitud termodinámica definida originalmente como criterio para predecir la evolución de los sistemas termodinámicos.

La entropía es una función de estado de carácter extensivo. El valor de esta magnitud física, en un sistema aislado, crece en el transcurso de un proceso que se da de forma natural. La entropía describe cómo es de irreversible un sistema termodinámico.

La palabra entropía proviene del griego y significa evolución o transformación.

En física, la entropía es la magnitud termodinámica que permite calcular la parte de la energía calorífica que no puede utilizarse para producir trabajo si el proceso es reversible. La entropía física , en su forma clásica, es definida por la ecuación.

o más simplemente, si la temperatura se mantiene constante en el proceso 1 → 2 ( proceso isotérmico ):

Así, si un cuerpo caliente a temperatura T1 pierde una cantidad de calor Q1, Su entropía disminuye en Q1 / T1, Si cede este calor a un cuerpo frío a temperatura T2 (inferior a T1)  la entropía del cuerpo frío aumenta más de lo que ha disminuido la entropía del cuerpo caliente porque

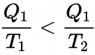
 Una máquina reversible puede, por tanto, transformar en trabajo una parte de esta energía calorífica, pero no toda.

El rendimiento que da la máquina reversible (que es el máximo que puede dar cualquier máquina) es:

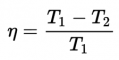
Para que toda la energía calorífica se pudiera transformar en trabajo sería necesario que, o bien el foco caliente se encontrara a una temperatura infinita, o bien que el foco frío estuviera a cero  kelvin; en otro caso, el rendimiento termodinámico de la máquina reversible es inferior a 1.

La expresión de la entropía es consecuencia lógica del segundo principio de la termodinámica y de la manera en que se mide la temperatura.

El  segundo principio de la termodinámica dice que, si no se consume trabajo, el calor de los cuerpos calientes a los cuerpos fríos, ya sea directamente por conducción como si se hace a través de cualquier máquina.

La temperatura hay que medirla en una escala termodinámica; de otro modo, la expresión de la entropía no es tan elegante y depende de la sustancia termométrica que se emplea para construir el termómetro. Al definir la escala termodinámica de temperatura, hay un grado de libertad que se puede escoger arbitrariamente. Si se impone que entre la temperatura de ebullición y la de congelación del agua haya 100 grados, se obtiene la escala Kelvin y resulta que la temperatura de congelación del agua debe ser 273 K.

Entropía de una suatancia pura

Cuando se tiene una sustancia pura, como el agua, que experimenta una variación de su temperatura, siendo la presión inicial y la final la misma, la variación de la entropía de la sustancia es, según la definición

Como proceso reversible podemos imaginar uno en el que la temperatura de la sustancia va variando gradualmente por igual en todos sus puntos, siendo la presión siempre la misma. En este caso

y la variación de entropía es

El calor específico es, en general, una función de la temperatura y debe ser tenido en cuenta a la hora de integrar. No obstante, si el rango de variación de la temperatura es pequeño, usualmente se puede aproximar c_p por una constante, su valor medio, y obtener la expresión

Combinado este resultado con el anterior, podemos trazar la gráfica de la entropía por unidad de masa, como función de la temperatura, para el agua desde el estado de hielo al de vapor, tomando como referencia el punto de fusión:

Cambio de entropía en procesos reversibles e irreversibles

Para calcular las variaciones de entropía de un proceso real (irreversible) hemos de recordar que la entropía (como la energía interna) depende solamente del estado del sistema. Una variación de entropía cuando el sistema pasa de un estado A a otro B de equilibrio depende solamente del estado inicial A y del estado final B.

Para calcular la variación de entropía ΔS de un proceso irreversible entre dos estados de equilibrio, imaginamos un proceso reversible entre el estado inicial A y el estado final B y calculamos para este proceso

ΔS=∫ABdQT${\displaystyle \Delta S={\displaystyle \underset{A}{\overset{B}{\int }}\frac{dQ}{T}}}$

Como veremos en los ejemplo, la variación de entropía ΔS es siempre positiva para el sistema y sus alrededores en un proceso irreversible.

La entropía de un sistema aislado que experimenta un cambio siempre se incrementa. En un proceso reversible la entropía del sistema aislado permanece constante.

Conducción térmica

 

En el proceso de conducción del calor, el sistema está formado por un foco caliente a la temperatura T_a conectado mediante una barra a un foco frío a la temperatura T_b. La barra hecha de un material conductor del calor está perfectamente aislada. Se transfiere a través de la barra una cantidad de calor Q del foco caliente al foco frío. Como el foco frío absorbe calor, su entropía aumenta en Q/T_b. Al mismo tiempo, como el foco caliente pierde calor su variación de entropía es -Q/T_a

 Como T_a>T_b, la variación de entropía del sistema formado por la barra y los dos focos es positivo

ΔS=QTb−QTa>0${\displaystyle \Delta S=\frac{Q}{T_b}-\frac{Q}{T_a}>0}$

Cambio de estado

Un sólido cuyo calor de fusión es L_f funde a la temperatura T_f. Calcular la variación de entropía cuando una masa m de sólido funde.

En el proceso de cambio de estado una sustancia absorbe una cantidad de calor mL_f manteniendo la temperatura constante T_f

ΔS=mLfTf${\displaystyle \Delta S=\frac{m{L}_f}{T_f}}$

Calorímetro de mezclas

En un calorímetro de mezclas, una sustancia de masa m₁ y calor específico c₁ y temperatura inicial T₁ se coloca en contacto con una segunda sustancia de masa m₂, calor específico c₂ y temperatura inicial T₂>T₁. Las dos sustancias se colocan en un calorímetro de modo que forman ambas un sistema aislado. Una vez que alcanzan el equilibrio térmico a la temperatura T_e vamos a calcular la variación de entropía.

La sustancia que inicialmente tiene la temperatura mas alta cede calor a la sustancia que inicialmente tiene temperatura más baja, la primera disminuye su temperatura, la segunda la aumenta hasta que ambas alcanzan el equilibrio a la temperatura T_e.

m₁·c₁·(T_e-T₁)+m₂·c₂·(T_e-T₂)=0

Te=m1c1T1+m2c2T2m1c1+m2c2${\displaystyle T_e=\frac{m_1{c}_1{T}_1+m_2{c}_2{T}_2}{m_1{c}_1+m_2{c}_2}}$

El proceso es irreversible por que el sistema evoluciona desde el estado inicial al final a través de una serie de estado de no equilibrio.

Para calcular la variación de entropía, podemos imaginar que la sustancia que tiene la temperatura más alta T₁ se enfría hasta una temperatura T_e poniéndola en contacto sucesivamente con focos de calor que difieren infinitesimalmente en temperatura, el primer foco tiene una temperatura T₂ y el último T_e. Podemos imaginar un proceso similar para la sustancia inicialmente a menor temperatura T₂.

El calor absorbido o cedido en un cambio infinitesimal de temperatura es

dQ=mcdT

ΔS=∫dQ1T+∫dQ2T=m1c1∫T1TedTT+m2c2∫T2TedTT=m1c1ln(TeT1)+m2c2ln(TeT2)${\displaystyle \Delta S={\displaystyle \int \frac{d{Q}_1}{T}}+{\displaystyle \int \frac{d{Q}_2}{T}}=m_1{c}_1{\displaystyle \underset{T_1}{\overset{T_e}{\int }}\frac{dT}{T}}+m_2{c}_2{\displaystyle \underset{T_2}{\overset{T_e}{\int }}\frac{dT}{T}}=m_1{c}_1\ln \left(\frac{T_e}{T_1}\right)+m_2{c}_2\ln \left(\frac{T_e}{T_2}\right)}$

Como T_e>T₁ el primer término es positivo, y como T_e<T₂ el segundo término es negativo, el resultado final es que ΔS>0

Expansión de un gas

Consideremos la expansión adiabática de un gas ideal que ocupa inicialmente un volumen V₁. Se rompe la membrana que separa el gas de la región en la que se ha hecho el vacío, el gas se expande irreversiblemente hasta ocupar un volumen V₂.

El trabajo realizado por el gas es cero W=0, y ya que las paredes del recipiente son aislantes, no se transfiere energía hacia el exterior, Q=0

Como la energía interna no cambia ΔU=0, la temperatura no cambia, ya que la energía interna de un gas ideal solamente depende de la temperatura T.

Para calcular la variación de entropía, podemos imaginar un proceso reversible isotérmico a la temperatura T en la que el gas empuje muy despacio el émbolo mientras la energía entra en el gas procedente de un foco de calor para mantener la temperatura constante.

ΔS=∫dQT=1T∫dQ${\displaystyle \Delta S={\displaystyle \int \frac{dQ}{T}}=\frac{1}{T}{\displaystyle \int dQ}}$

En un proceso isotérmico, no hay variación de energía interna, el primer principio implica que el calor absorbido es igual al trabajo realizado por el gas durante su expansión de V₁ a V₂.

dQ=dW=pdV

ΔS=1T∫V1V2pdV=∫V1V2nRVdV=nRlnV2V1${\displaystyle \Delta S=\frac{1}{T}{\displaystyle \underset{V_1}{\overset{V_2}{\int }}pdV=}{\displaystyle \underset{V_1}{\overset{V_2}{\int }}\frac{nR}{V}dV=}nR\ln \frac{V_2}{V_1}}$

Como V₂>V₁ se concluye que ΔS>0

Páginas consultadas:

http://www.sc.ehu.es/sbweb/fisica_/estadistica/termodinamica/segundo/segundo1.html#:~:text=Una%20variaci%C3%B3n%20de%20entrop%C3%ADa%20cuando,y%20del%20estado%20final%20B.&text=La%20entrop%C3%ADa%20de%20un%20sistema,del%20sistema%20aislado%20permanece%20constante.

http://laplace.us.es/wiki/index.php/Entrop%C3%ADa#Calentamiento_de_una_sustancia_pura